Persistent Path Planning

Project description: As robotic technology improves, there has been an increase in the use of robotic technology for tasks such as data collection in marine environments. While it is currently possible for robotic missions to occur with pre-planned instructions, these missions do not have the ability to account for changes in the environment that may change the objective of the mission. This is particularly relevant in maritime mission domains, where the environment dynamics change across space and time (for example, ocean currents).

Current data collection technology in maritime environments are either capable of persistent missions in a fixed location, or are capable of collecting data over a restricted time and domain. As such, as part of my research, I explore the use of renewably-powered autonomous sailing drones for persistent missions in maritime environments (notably the Gulf Stream off the coast of North Carolina).

The first step in my research involved the exploration of a method for first planning for persistent missions. To do this, I conducted a literature survey of various path-planning algorithms, from which I identified the A* algorithm to be a particularly useful algorithm. I then implemented it into a persistent mission as I lay out below.

Setup

The mission domain is represented by an NxN grid of locations. Each location is associated with a position identifier (latitude and longitude) as well as a measure of “coverage” (between 0 and 1) at that location.

Coverage is defined as a measure of how much information is known at a given location. It is also defined as a measure of the quality of the information at a given location.

To test the algorithm, described below, we initialize the mission domain with random coverage at each location. We then initialize the boat at the location with the highest coverage in the domain. From there, we run the algorithm while keeping track of the total coverage in the domain. The algorithm is successful if the planned path travels through areas of low coverage, while also gaining coverage over time.

The Algorithm

My approach to persistent planning involves a two-step process that runs repetitively. The first of the steps is a goal-selection algorithm. Once a goal is selected, this is fed into a custom implementation of the A* path-planning algorithm.

Goal Selection

The goal is selected with two main factors:

Distance from current location
Coverage at goal location

Each location in the domain is evaluated using the following formula:

$k_1(1-Q) + k_2D$

where $k_1, k_2$ are weights, $Q$ represents the coverage at each location, and $D$ represents the distance from the current location to each location.

The location that yields the highest value for the above functio is chosen as our goal. By doing so, we ensure that we choose a location that is both sufficiently far away and will gain a large amount of coverage. By traversing farther away from our current location, by necessity, we will visit more locations in the domain, thus increasing the coverage gained.

A*

The A* algorithm is a graph-traversal algorithm that optimizes using edge and node costs alongside a heuristic. It is commonly used for path-planning in robotics, where the domain is converted in a traversable graph, and distances represents costs. The logic is explained in the animation below.

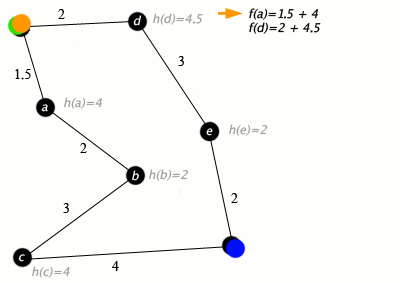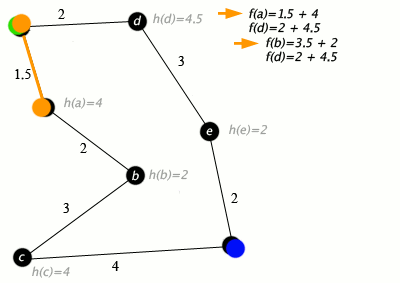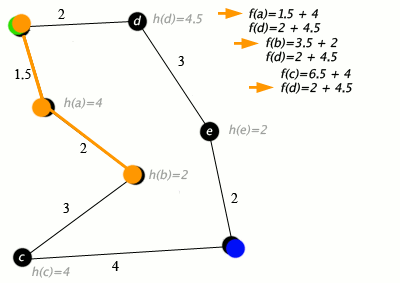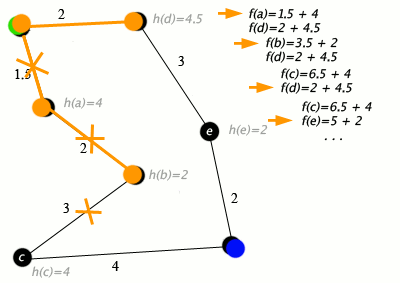
In my implementation, I modify the graph such that the cost at each node(location in our domain) is the coverage at that location and the edge cost is the distance between each location. The heuristic is a distance-to-go measure, which accounts for the distance from the current node to the goal node. This ensures that we minimize the cost, which in turn results in the maximization of coverage gained while still maintaining progress towards the goal location.

Results

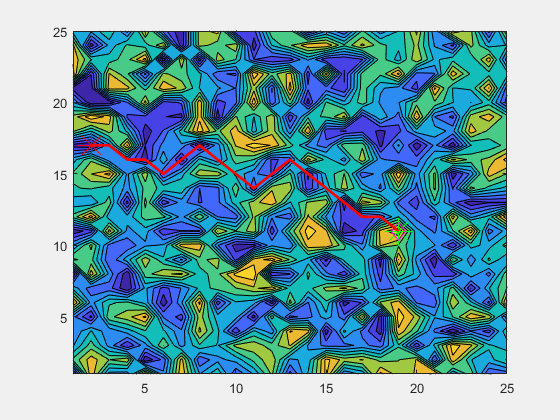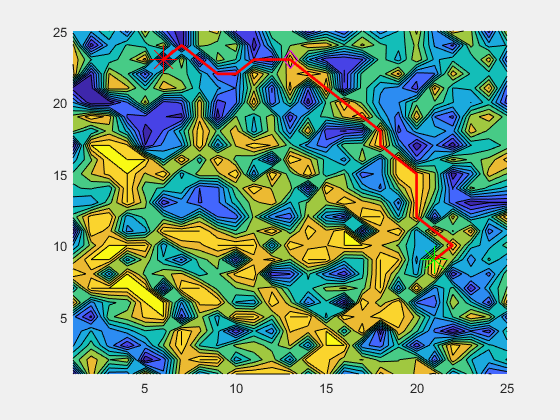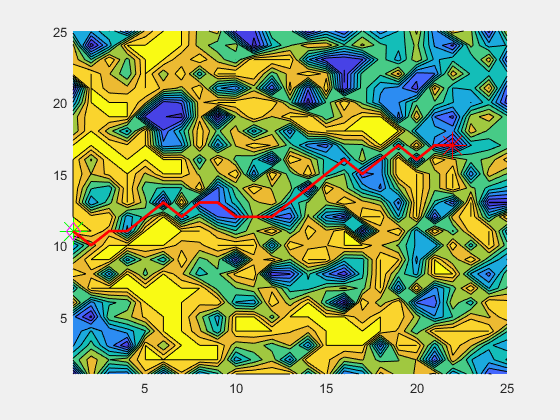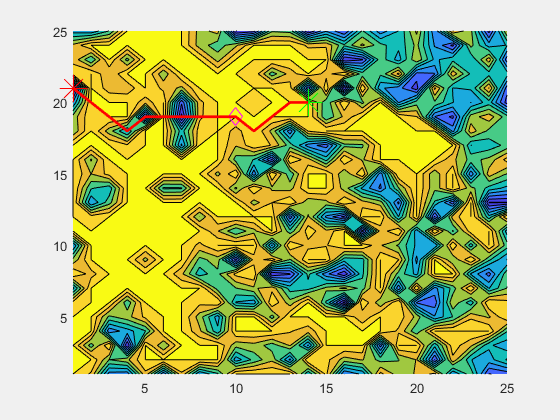
The above animation shows the algorithm in work. The diamond represents the current location of the boat/agent. The green star represents the location where the boat was when the current goal was calculated. The red star represents the current goal. The red line represents the path calculated by the A* algorithm.

Ongoing/Future Work

My current work builds on this initial A* implementation by including more realistic dynamics in the environment and improving the dynamic model of the boat that is traversing the domain. I am currently working on adapting the algorithm to also account for variation in ocean currents and available solar power.